Rotation Matrices
A 3D rotation matrix is of size is 3X3 and is given as below,

I will clear your doubts on rotation matrices using below example.
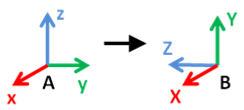
Lets assume we have two frames A and B. Frame A is denoted by x,y,z axes and frame B is denoted by X,Y,Z axes.

Fig. 1 Frame A and Frame B
To get the rotation of frame B w.r.t frame A we have to find the unit vectors [X,Y ,Z] of X,Y,Z coordinate axes in terms of [x,y,z] unit vectors of x,y,z coordinate axes.
The unit vectors [X,Y,Z] of frame B can be written in terms of unit vectors [x,y,z] of frame A as given below

So as you see in the above equation , R11,R12,.......R33 are the 9 variables that describe the orientation of frame B w.r.t frame A.
Hence these 9 variable can be grouped into 3X3 matrix, where each column represent the target frame unit vector [X,Y,Z] .

To find R11,R12,.......R33 we have to super impose frame B on frame A. I have split the diagrams for each unit vector of frame B

Fig. 2 Representing Frame B unit vectors in terms of Frame A unit vectors
Coming to the calculation of R11,R12,......R33, you need to superimpose two frames and find them as shown in fig 2.
The elemental rotations along x-axis, y-axis and z-axis by angle α, β and ɣ respectively are given as below


Hope now you are clear with rotation matrices and its elements.
You can find the rotation matrix intuitively by seeing the source frame and target frame
I will explain you how, with some examples.
1).
2).

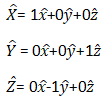



Now its your turn to find the below rotation matrices.

Thanks for reading. For any queries please comment below.